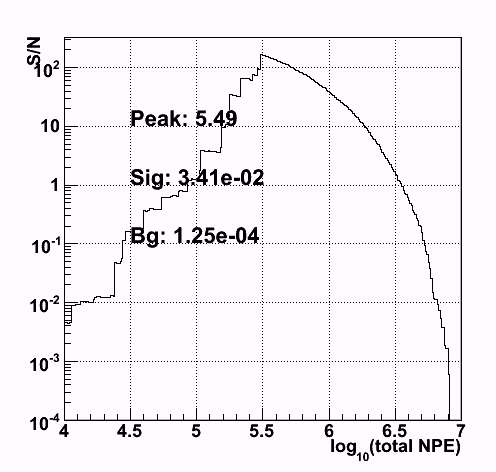
example of the signal to background ratio
(-0.1 < cos(ZA) < 0.1)
Cut position for each zenith angle
At first the cut position is roughly determined by searching the position where the signal to background ratio becomes maximum. Note that I fixed the background amount to 1.e-4/(0.1*cos(ZA)) if the background becomes less than the amount.
The example of the signal to background ratio is shown below.
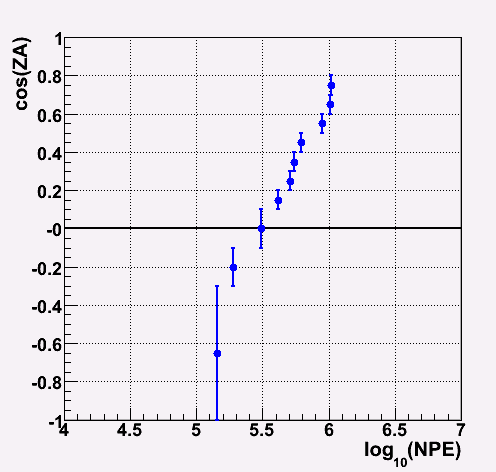
The determined rough cut points are shown below.
|
example of the signal to background ratio 
|
Cut position for each zenith angle 
|
After determining the rough shape, I made several lines to express the shape as shown below. (Actually, the lines indicate the optimized the cuts.)
|
Background 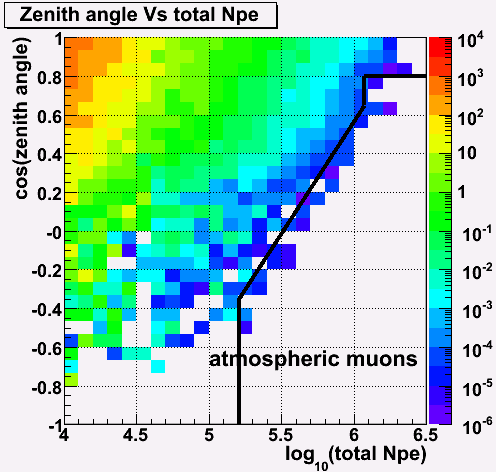
|
EHE signal 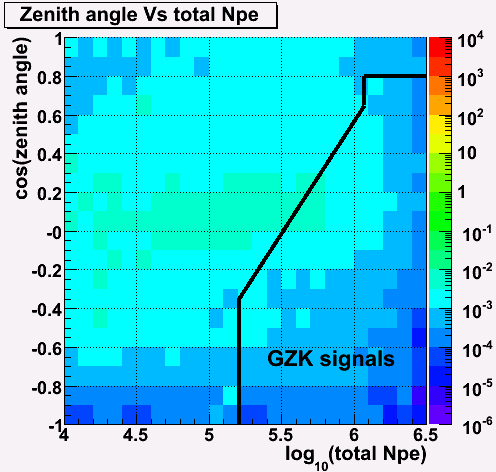
|
Real data 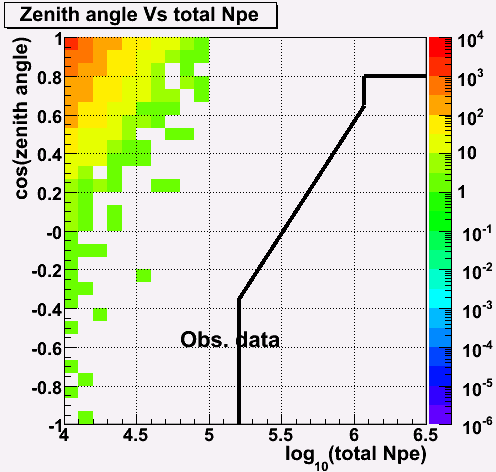
|
Then, I shifted the lines in NPE direction. I took the Npe shift (0.05) in order to keep the signal to background ratio of 200. (In the above plots, this Npe shift is already taken into account.)
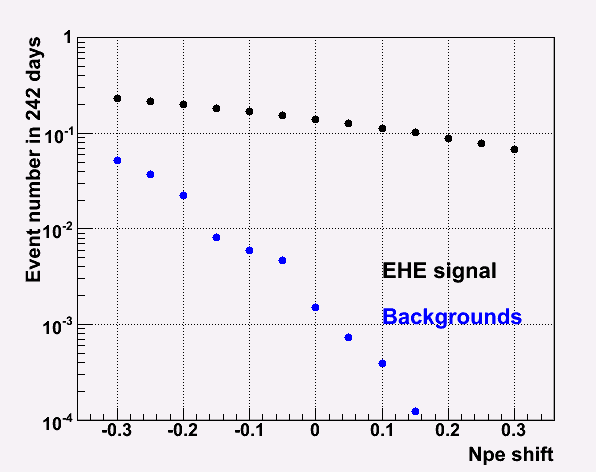
|
NPE distribution before and after cut 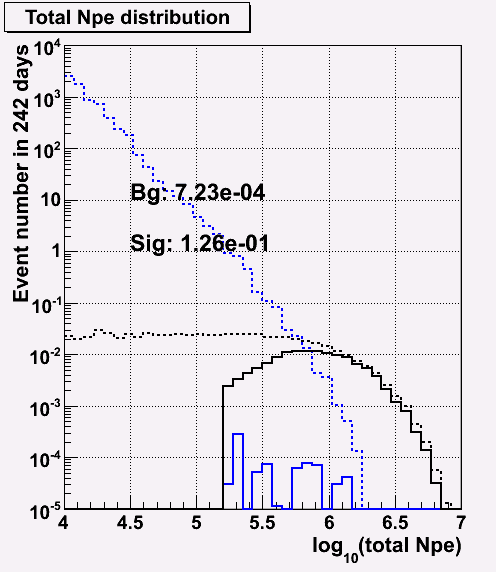
|
ZA distribution before and after cut 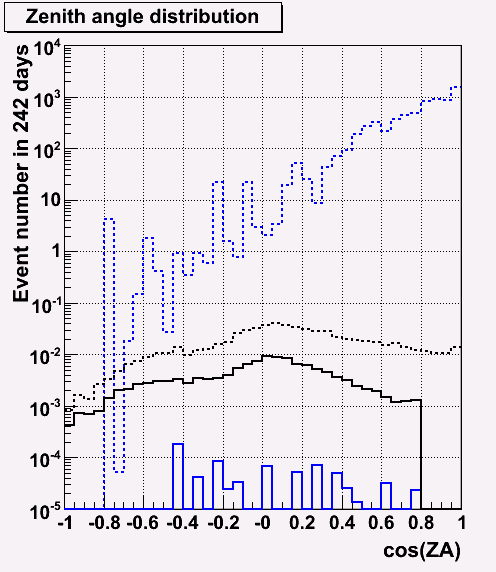
|
Energy distribution before and after cut 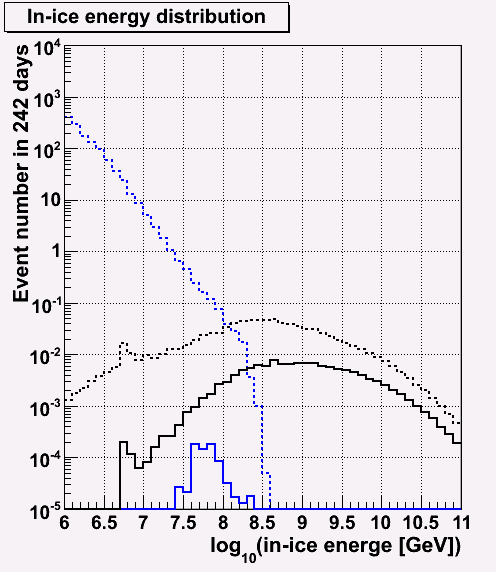
|
It turned out that there is a place that events tend to be mis-reconstructed horiontally where the ice is clean. Therefore, I divide the events into two groups by the CoGZ position.
One is -50 < CoGZ < 50 m and CoGZ < -250 m where the ice is relatively clean, and the another is other CoGZ position, namely CoGZ > 50 m and -250 < CoGZ < -50 m.
|
CoGZ Vs ZA (empirical model) 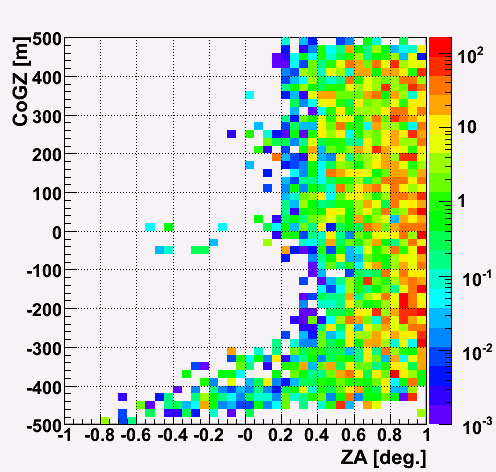
|
CoGZ Vs ZA (obs. data) 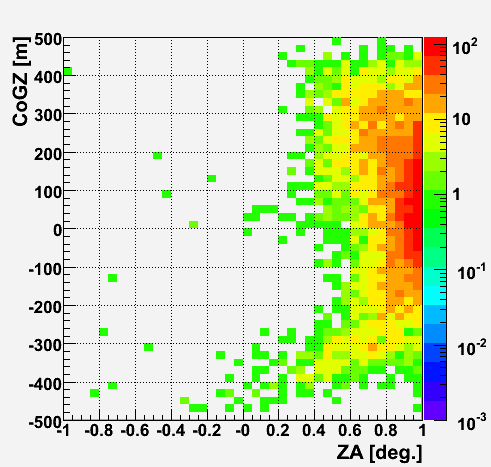
|
The cut is optimized in the same way as mentioned above.
The determined rough cut points are shown below.
|
Cut position for each zenith angle 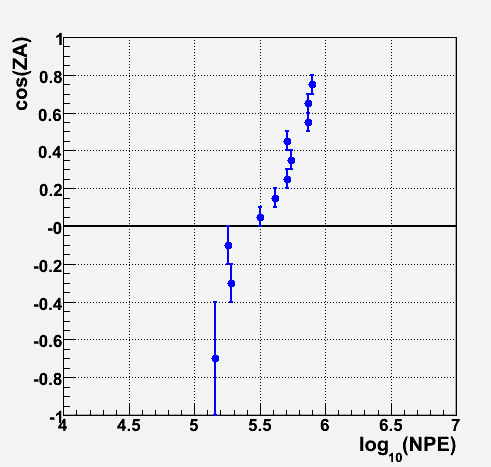
|
Cut position for each zenith angle 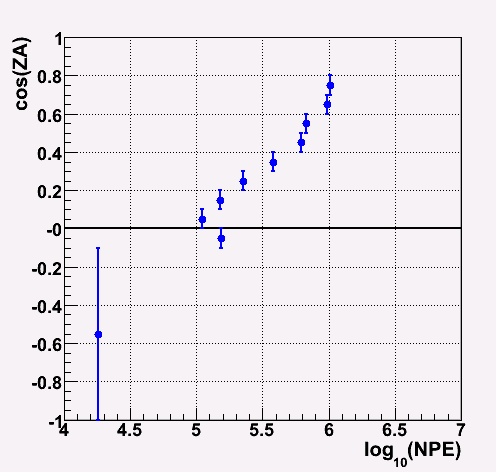
|
|
Background 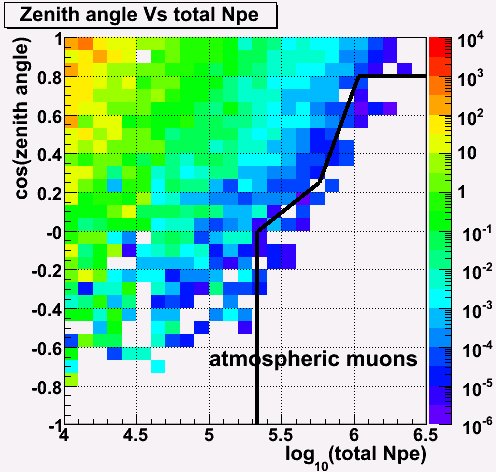
|
EHE signal 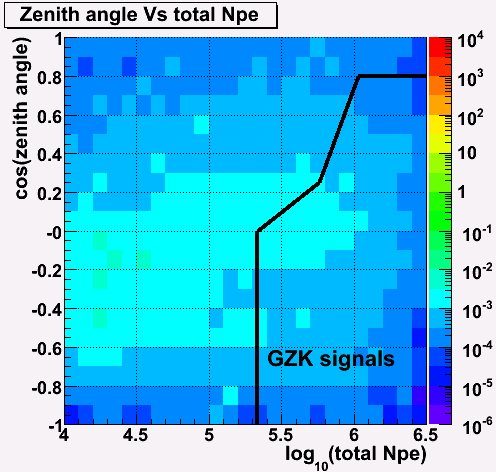
|
Real data 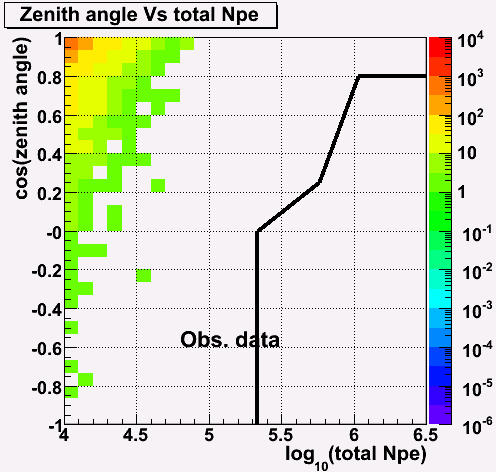
|
|
Background 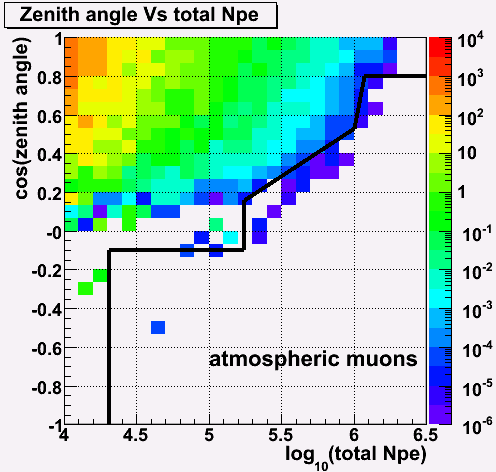
|
EHE signal 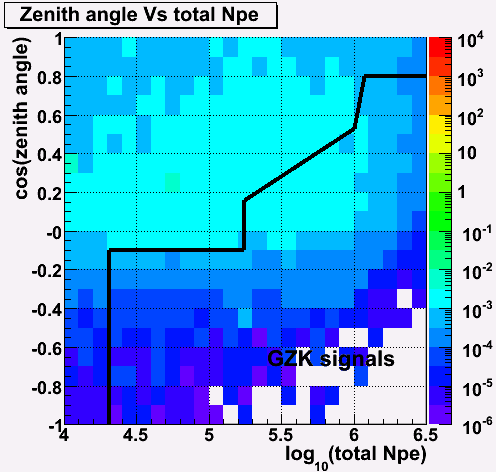
|
Real data 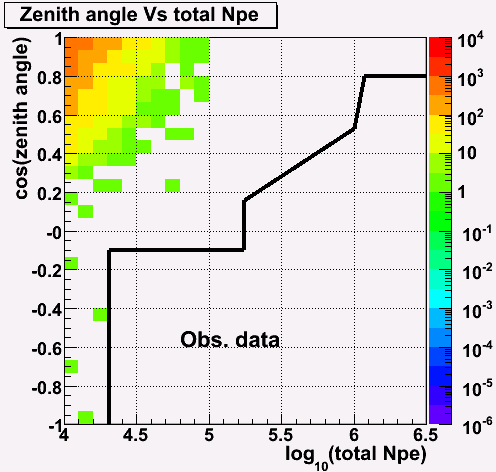
|
|
optimization 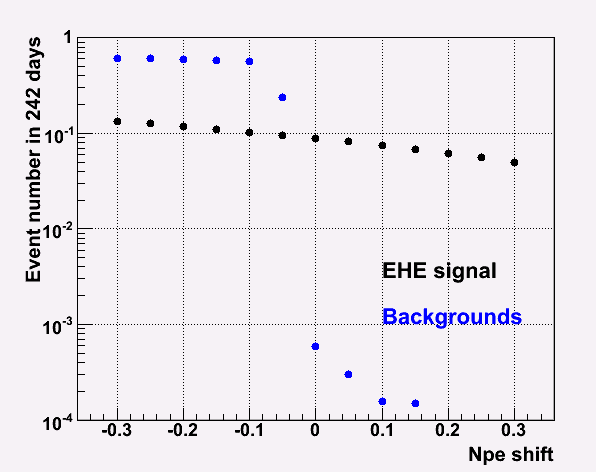
|
optimization 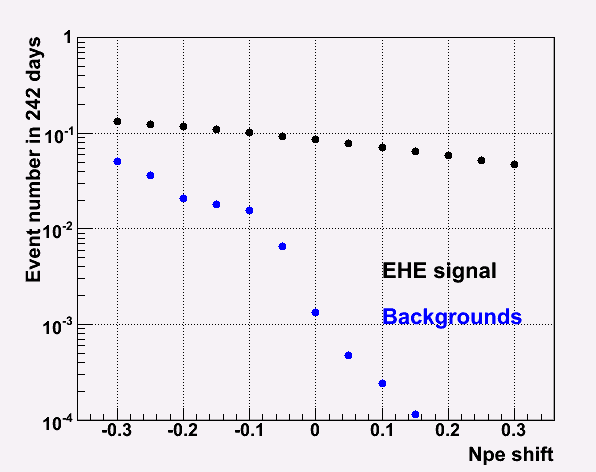
|
|
NPE distribution before and after cut 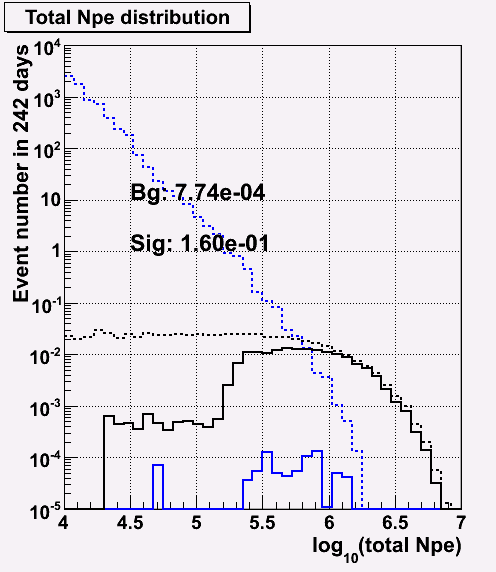
|
ZA distribution before and after cut 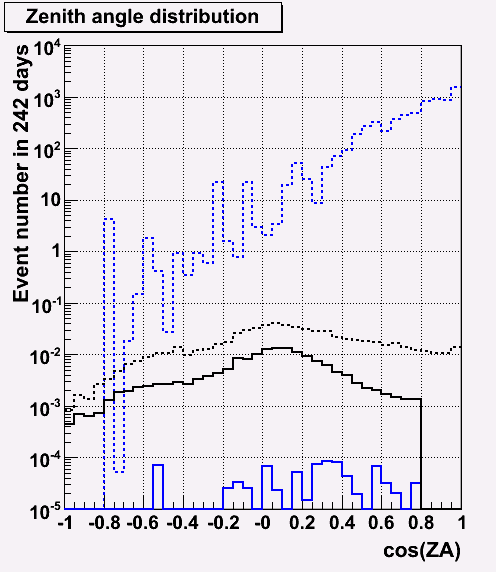
|
Energy distribution before and after cut 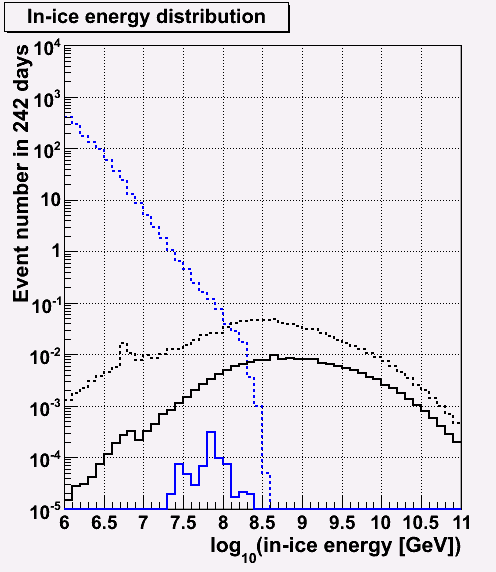
|
|
NPE distribution before and after cut 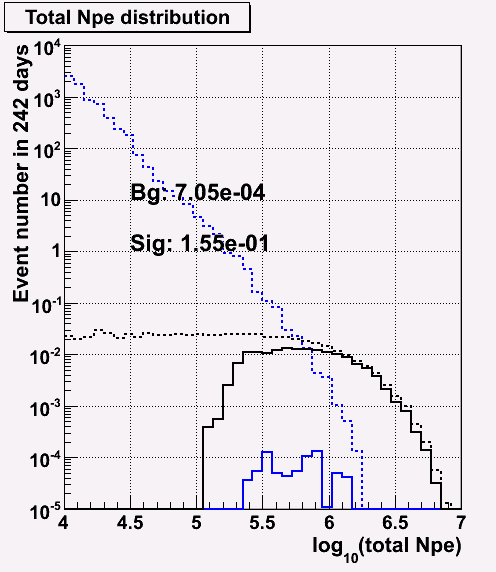
|
ZA distribution before and after cut 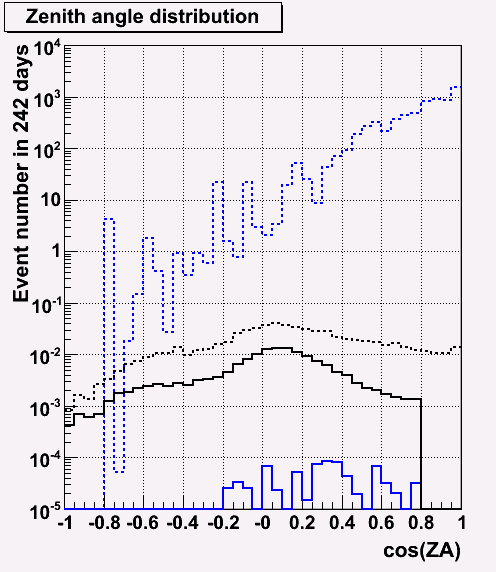
|
Energy distribution before and after cut 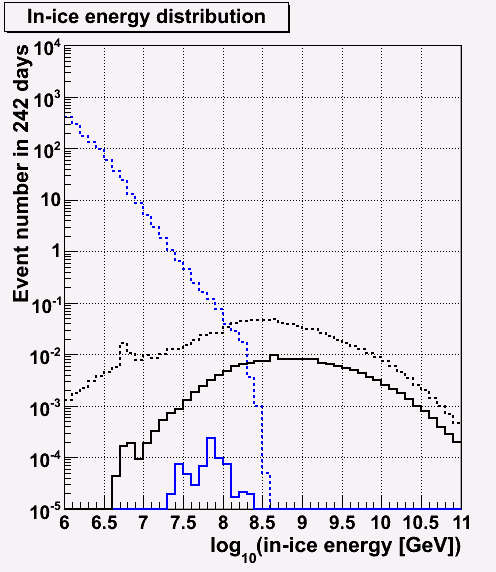
|
|
Sensitivity 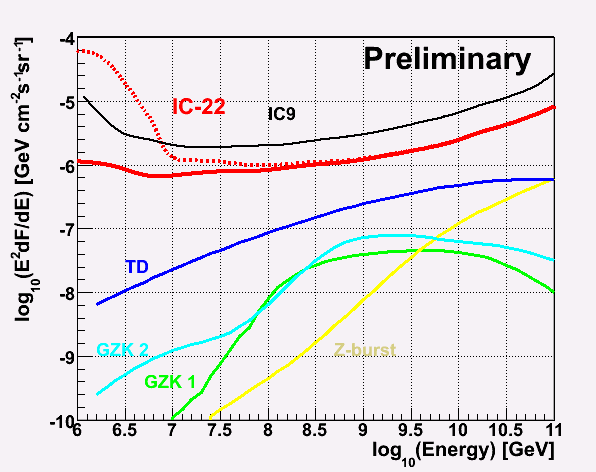
|
|
Total effective area (all flavor sum (nu_e+nu_mu+nu_tau) 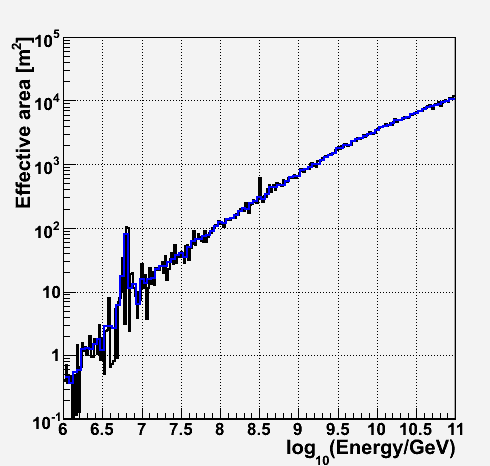
|
Sensitivity 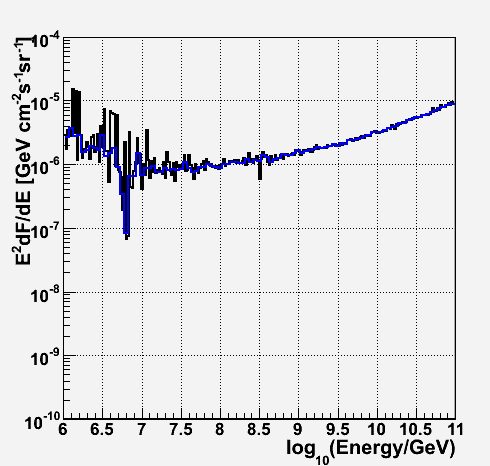
|
|
Sensitivity 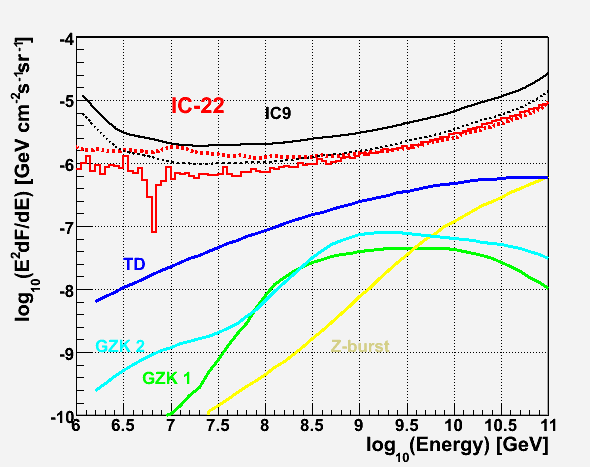
|
|
Effective area (all flavor sum (nu_e+nu_mu+nu_tau)) 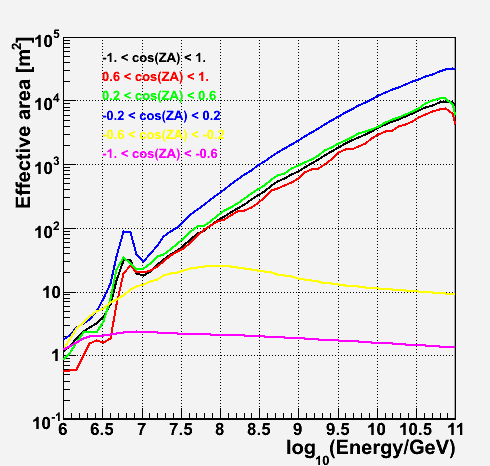
|
Keiichi Mase Last modified: 2009-02-18 15:44:59