black: obs. data, blue: empirical model, magenta: corsika(iron)
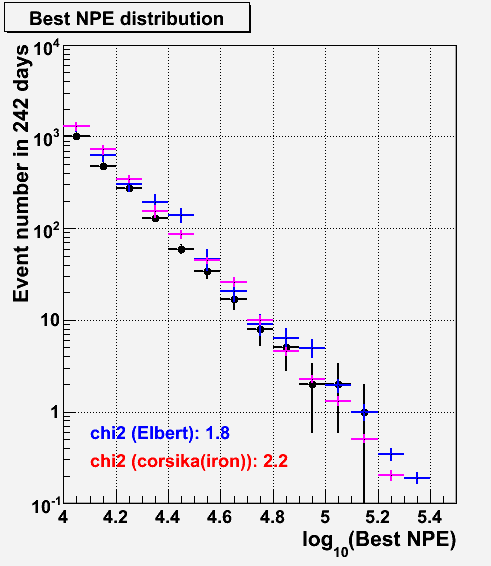
black: obs. data, blue: empirical model, magenta: corsika(iron)
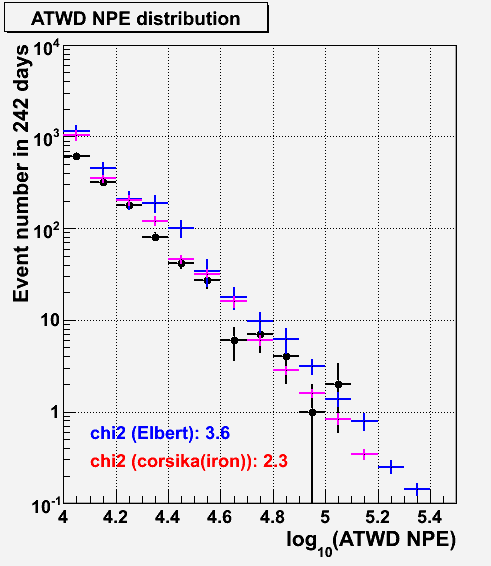
black: obs. data, blue: empirical model, magenta: corsika(iron)
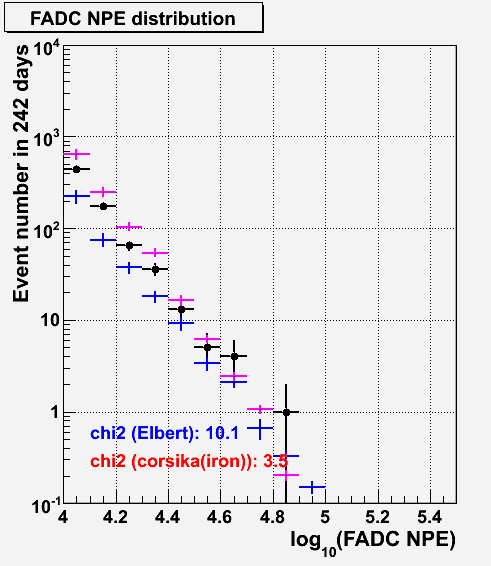
J. A. Aguilar found that there is a problem in FADC. Have a look at this presentation.
We have used the DOMcalibrator without the droop correction, therefore, in principle our analysis is not affected by the bug.
Although, I have checked the NPE distributions for best, ATWD and FADC NPEs. The NPE here is an event-wise NPE, summing up all NPE of each detector for an event. The best NPE is the event-wise total NPE by taking the larger ATWD or FADC for a DOM.
We found ~50 % difference in case of FADC for the empirical model in the event rate. Therefore, the NPEs from FADC could be underestimated in the empirical model, but this is not true. This is because we use the best NPE and we fit the observational data with the best NPE, therefore, the effect of the difference in FADC is absorbed by the fit. (Look at the ATWD distribution. The empirical model is higher than the data to compensate the FADC difference.)
Those distributions of FADC/ATWD are cases we only used the ATWD and FADC. However, the best NPE is the combination of ATWD/FADC, taking the higher value for each DOM, and ATWD gives higher NPE contributions compared to the FADC NPE. Therefore, the effect of this difference is minimal for our analysis. Let me remind that the empirical model uncertainty is enough large (~100%) compared to this difference.
This difference will underestimate the signal NPE, so this is safer side.
This difference will be explained by the difference of the bundle nature. Looking at the FADC NPE distribution the data is bracketed by the empirical model and the CORSIKA. This may mean that the observational data express somewhere middle of the empirical model (single muon assumption) and the CORSIKA bundles.
|
black: obs. data, blue: empirical model, magenta: corsika(iron) 
|
black: obs. data, blue: empirical model, magenta: corsika(iron) 
|
black: obs. data, blue: empirical model, magenta: corsika(iron) 
|
Keiichi Mase Last modified: Thu May 29 02:22:42 JST 2008