
We are measuring the charge response and waveform of PMT using single photo-electron events.
Our findings are:
These delightful news encourage us to develop fast PMT simulator named "ROMEO" - the Root-based Optical Module EmulatOr.
In this page, we show the results regarding the development of our new simulator.
Update records:
![]()
Contents:
![]()
| MODULE NAME | MODEL | COMPANY | NOTES |
| Function Generator | 33120A | Agilent Technology | |
| Oscilloscope | TDS2012 | Tektronix | 2ch, digital strage |
| ADC(Analog to Digital Converter) | 2249A | LeCroy | 0.25pC/bin, |
| Crate controller | CC/7700 | Toyo technica | |
| Dual gate generator | KN1500 | Kaizu Works | |
| 8ch Discriminator | N-TM405 | Technoland | |
| 4-hold 1-veto coincidence | 470 | Kaizu | |
| Quad high voltage | RPH-22 | Repic | |
| 16ch TTL-NIM Level Adopter | KN206 | Kaizu Works | |
| Preset scaler controller | 150 | Kaizu | |
| Dual variable delay | 330 | Kaizu |
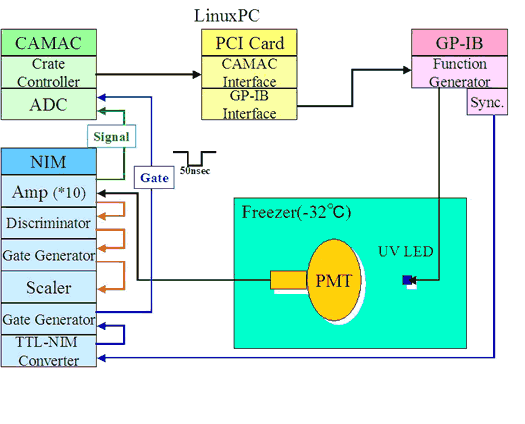
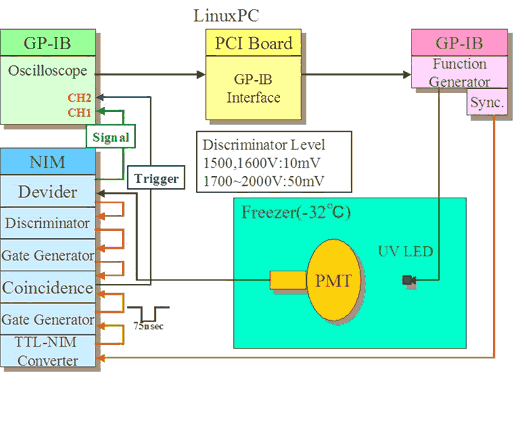
[top]
![]()
The most simplest formula to represent the signal part of ADC spectrum(single p.e.) can be easily supposed to be a gaussian function. However, our data shows the existence of another component: exponential-like component appears together with the main gaussian feature and dominates especially at lower ADC range. This behavior probably arises from the instability of first dynode gain.
We thus sum up both components and assumed it to be a model function of our data. Reduced fitting chi-square between our data and model were below 1.0, which justify our model assumption.
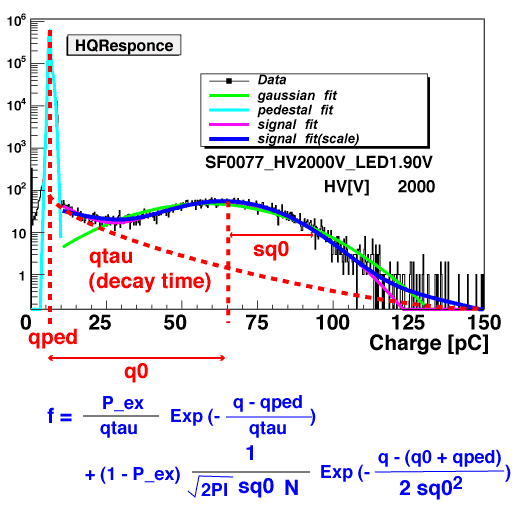
(fig1)
[top]
![]()
Fitted gain(calculated from q0), sq0, and qtau of different PMTs are shown in fig2.
It indicates that the model parameters like sq0 have apparent correlation with gain. If they indeed scale with gain, i.e. the signal function is scaling with gain, the PMT gain gives all the model parameters uniquely.
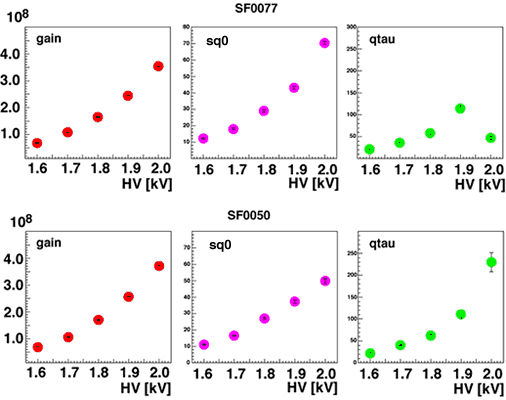
(fig2)
[top]
![]()
Below are the ratio of sq0/q0 and qtau/q0 as a function of HV. Note that sq0/q0 corresponds to charge resolution. They seem independent of HV implying that the signal function is indeed scaling with the PMT gain.
It allows that only the one parameter, q0, which is obtained by charge histogram, fully to describe the SPE resolution function because the other parameters are automatically determined with q0, i.e. the PMT gain.
This advantage plays a key role in the DOM Monte-Carlo simulator.
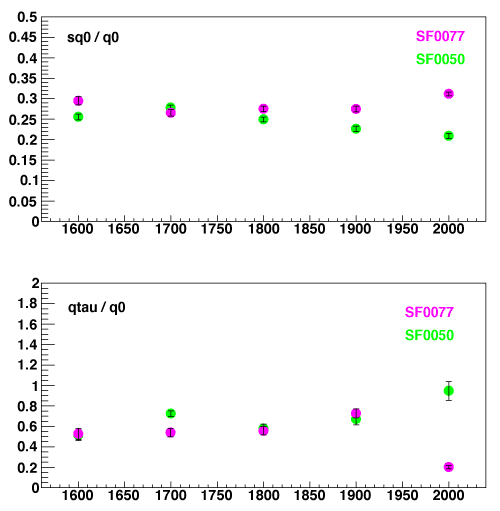
(fig3)
[top]
![]()
We tried to fit the output waveform taken by a digital oscilloscope(Tektronix, TDS2012).
Simple gaussian form would represent our data well except for the ringing tail which should be fixed sooner or later.
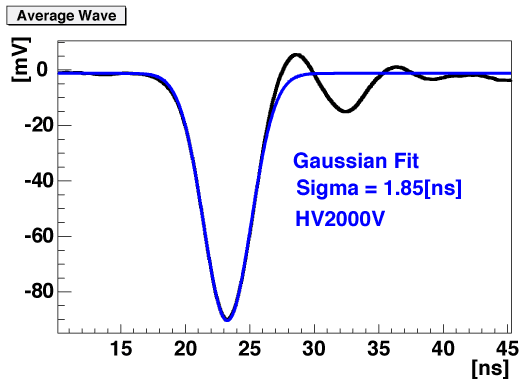
[top]