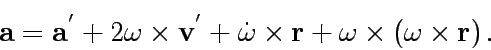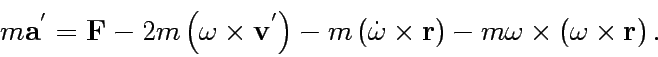Next: Solution Example II
Up: mechanics
Previous: mechanics
We first consider the vector transformation from the coordinate system
K to the co-rotational system K'.
The pointer vector 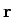 is represented by
the linear combination of the unit vector
is represented by
the linear combination of the unit vector 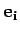 (
(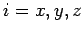 )
in K:
)
in K:
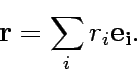 |
(1) |
Equally one can write
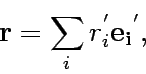 |
(2) |
in the co-rational system K'.
The time differential of the unit vectors in K'
is given by
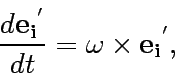 |
(3) |
where 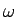 is the angler velocity vector.
When the differential operator
is the angler velocity vector.
When the differential operator 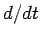 is applied
in equation (2),
the relation (3) above gives
is applied
in equation (2),
the relation (3) above gives
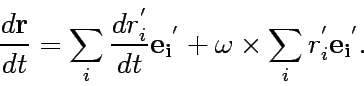 |
(4) |
Here the first term in the right hand side above
is the velocity seen by the observer in the co-rational
system K'. Consequently the equation (4)
can read
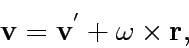 |
(5) |
where 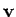 is the velocity vector.
is the velocity vector.
The acceleration 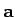 in K is then obtained
by the time differential of the equation (4)
as
in K is then obtained
by the time differential of the equation (4)
as
Here we used the relation (3).
The first term in the right hand side in the equation above
represents the accelerator for the observer in K'.
We, therefore, finally get
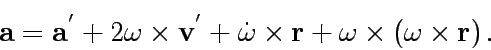 |
(7) |
The equation described above and
the Newtonian equation of the motion
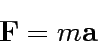 |
(8) |
then lead to the following final equation
of the motion for the observer in k';
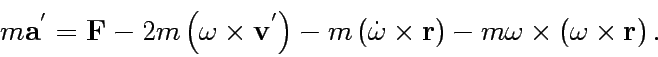 |
(9) |
The terms in the right hand side imply
the external force, the coliori Force, the apparent force
due to the angular (de-)acceleration, and the centrifugal force,
respectively.



Next: Solution Example II
Up: mechanics
Previous: mechanics
Shigeru Yoshida
2003-01-15
![]() is represented by
the linear combination of the unit vector
is represented by
the linear combination of the unit vector ![]() (
(![]() )
in K:
)
in K:
![]() in K is then obtained
by the time differential of the equation (4)
as
in K is then obtained
by the time differential of the equation (4)
as