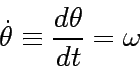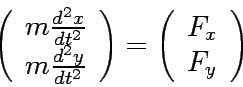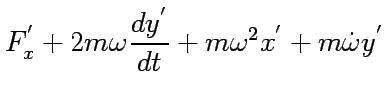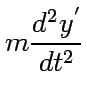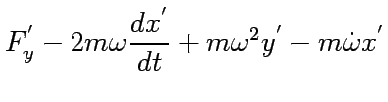Next: About this document ...
Up: mechanics
Previous: Solution Example I
Let us define the z-axis equal to to the direction
of the angular velocity vector 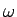 .
The variables in the coordinate system K
and those in the co-rotational system K'
are related by the rotation matrix as
.
The variables in the coordinate system K
and those in the co-rotational system K'
are related by the rotation matrix as
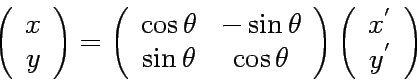 |
(10) |
where 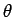 is an angle between
is an angle between 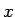 -axis in K
and
-axis in K
and 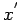 -axis in K'.
Note that
-axis in K'.
Note that
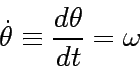 |
(11) |
and
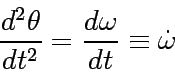 |
(12) |
Then the time differential operation applied in
the equation (10) gives
Here we occasionally used the relation (10)
whenever applicable.
Multiplication of the inversed rotation matrix from left-side
to the equation above then leads to
Using the Newtonian equation of motion
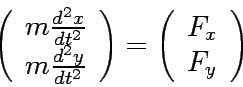 |
(14) |
where 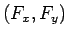 is the external force of
the x and y component, respectively, and
is the external force of
the x and y component, respectively, and
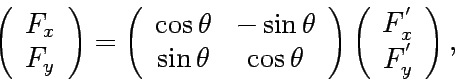 |
(15) |
we finally obtain
One finds the apparent force term by 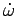 .
.



Next: About this document ...
Up: mechanics
Previous: Solution Example I
Shigeru Yoshida
2003-01-15
![]() .
The variables in the coordinate system K
and those in the co-rotational system K'
are related by the rotation matrix as
.
The variables in the coordinate system K
and those in the co-rotational system K'
are related by the rotation matrix as