The Thomson scattering describes photon scattering by free electrons in the classical electricity and magnetism. This is an approximation in the low energy limit where the quantum effect is no longer significant.
Let me first remind you of some fundamental equations of the classical
electricity and magnetism involving the photon radiation.
In the system with a charge density ![]() and its current
and its current ![]() (see the FIG. 1),
the Maxwell equations give the electric scalar potential
(see the FIG. 1),
the Maxwell equations give the electric scalar potential ![]() and the vector potential
and the vector potential ![]() as
as
The solutions of the equations above describe the famous
delayed potential:
When ![]() , then
, then
![]() , and the radiation
fields are considered to be plane waves. Then only the vector potential
, and the radiation
fields are considered to be plane waves. Then only the vector potential
![]() describes everything because
describes everything because
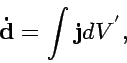 |
(6) |
Now let us consider the system that consist of an electron
in the external field ![]() and
and ![]() .
In the quantum picture, these fields correspond to a photon,
which implies the interactions between a photon and an electron.
When non-relativistic case,
.
In the quantum picture, these fields correspond to a photon,
which implies the interactions between a photon and an electron.
When non-relativistic case, ![]() , the electrical force
is by far larger than the Lorentz force. Then the equation of
motion of an electron gives
, the electrical force
is by far larger than the Lorentz force. Then the equation of
motion of an electron gives
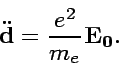 |
(9) |
| (11) |