![\begin{figure}\centering\includegraphics[width=.6\textwidth]{eddington.eps}
\par\end{figure}](Timg55.png) |
One of the representative astrophysical application of the Thomson scattering is the Eddington Limit, the possibly maximum luminosity of a star, which can keep electrons from being blown out of the sphere.
As shown in FIG. 2, a free electron
can maintain within the sphere when the radiation pressure
is weaker than the gravitational force falling into the star center.
The radiation (photon ) energy flux at distance ![]() from the center of the star is
from the center of the star is
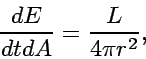 |
(14) |
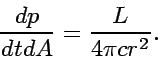 |
(15) |
Then the momentum transfer rate, i.e. the radiation force to a free electron is given by
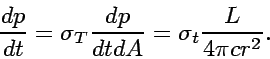 |
(16) |
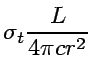 |
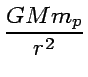 |
||
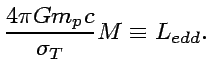 |
(17) |
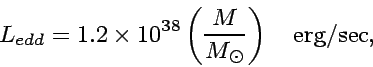 |
(18) |