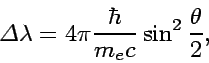Compton Scattering

In the Thomson scattering, the classical picture of the photon-free-electron scattering, there would be no change of energy of the electromagnetic field. In other word, the frequency/wavelength of light should maintain same before and after the scattering. In 1924, Compton observed scattering between X-ray and electrons where wavelength of the scattered light becomes larger than its initial value by

$$\Delta \lambda = 4\pi {\hbar\over m_e c}\sin^2{\theta\over 2},$$ (20)

which appears to be inconsistent with the classical theory.

Figure 4: Photon colliding to a rest electron.

This apparent inconsistency turned out to be understood in the Quantum picture where the radiation field is equivalent to a photon. In the system illustrated in FIG. 4, The energy momentum conservation leads to the following equations:

$$\epsilon + m_ec^2 = \epsilon^{rec} + E^{rec}$$

$$\epsilon = \epsilon^{rec}\cos\theta + \sqrt{E^{rec^2}-m_e^2c^4}\cos\phi$$

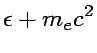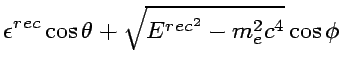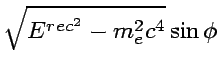$$\epsilon^{rec}\sin\theta = \sqrt{E^{rec^2}-m_e^2c^4}\sin\phi$$ (21)

Finally we get the recoiling photon energy as

$$\epsilon^{rec} = \epsilon{1\over 1+ {\epsilon\over m_ec^2}(1-\cos\theta)}$$ (22)

and $1-\cos\theta=2\sin^2(\theta/2)$ indeed gives Eq. 20.

It should be remarked that the recoiling energy given by Eq. 22 can be easily obtained by the 4-momentum treatment in the scheme of the relativistic kinematics. The photon 4-momentum vector $k=(\epsilon/c,{\bf p})$ and the electron 4-momentum vector $P=(E/c, {\bf P})$ follows the conservation law in the collision such as

$$k + P = k^{rec}+P^{rec}.$$ (23)

Then

$$P^{rec,2}= m_ec^2 = (k+P-k^{rec})^2$$ (24)

and using that $k^2=k^{rec,2}=0$ and that the momentum component of $P$ vanishes as the initial electron is at rest leads to Eq. 22.

The cross section of the Compton Scattering is described by the Kline-Nishina Formula:

$${d\sigma\over d\cos\theta} = {3\over 8}\sigma_T \left({1\over 1+ {\epsilon_{\gamma}^{'}\over m_ec^2}(1-\cos\theta)}\right)^2$$

$$\times [\left({1\over 1+ {\epsilon_{\gamma}^{'}\over m_ec^2} (1-\cos\theta)}\right) +1+ {\epsilon_{\gamma}^{'}\over m_ec^2}(1-\cos\theta)$$

$$-\sin^2\theta],$$ (25)

$^{'}$ implies the valuables described in the electron rest system.