

Next: Pair Creation
Up: Compton Scattering
Previous: Compton Scattering
When an electron is not at rest, but colliding with a soft photon,
the recoiling photon gains its energy by the transfer from the incoming
electrons.
This process called Inverse Compton Scattering,
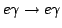 , is a representative radiation in many astronomical
environments that produces high energy X-ray/
, is a representative radiation in many astronomical
environments that produces high energy X-ray/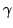 -ray.
-ray.
The colliding energy between a photon and an electron
is often defined by the he Lorentz invariant
center of mass (CM) energy squared 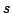 as defined by
as defined by
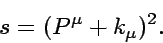 |
(26) |
Here
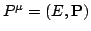 and
and
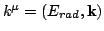 are 4-momentum of the electron and the photon respectively.
are 4-momentum of the electron and the photon respectively.
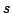 can be rewritten in the different system:
can be rewritten in the different system:
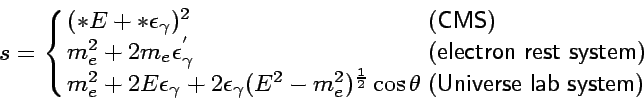 |
(27) |
Here natural unit is used i.e. 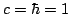 .
In this expression, the photon energy
.
In this expression, the photon energy
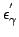 in the electron rest system in Eq. 25
is written by
in the electron rest system in Eq. 25
is written by
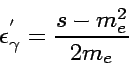 |
(28) |
in the Lorentz invariant form.
The Lorentz transformation gives the relations between energies
in the electron rest system and those in Universe lab system
when incoming electron energy is by far higher than
the target photon. Then
one can calculate energy of the recoiling electron 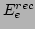 as a function of incoming electron energy
as a function of incoming electron energy 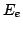 in the lab system as
in the lab system as
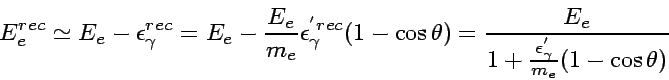 |
(29) |
where
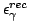 is the recoiling energy of
is the recoiling energy of 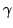 -ray
in the Universe lab system.
By using Eq. 29
we can modify the Kline-Nishina
formula Eq. 25
to derive the energy differential
cross section. We obtain
-ray
in the Universe lab system.
By using Eq. 29
we can modify the Kline-Nishina
formula Eq. 25
to derive the energy differential
cross section. We obtain
Here
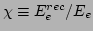 is the dimensionless energy of the electron
normalized by primary energy of incoming electron.
The electron transfer most of its
energy to the photon via the inverse Compton scattering
as you see the cross section becomes larger in
is the dimensionless energy of the electron
normalized by primary energy of incoming electron.
The electron transfer most of its
energy to the photon via the inverse Compton scattering
as you see the cross section becomes larger in 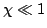 regime
in Eq. 30.
Integrating
regime
in Eq. 30.
Integrating 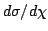 from
from 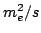 to 1
(this range is given by Eq. 29
with
to 1
(this range is given by Eq. 29
with
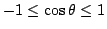 ), we obtain the total cross section:
), we obtain the total cross section:
where
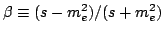 is the velocity
of the outgoing electron in the CMS.
is the velocity
of the outgoing electron in the CMS.


Next: Pair Creation
Up: Compton Scattering
Previous: Compton Scattering
Shigeru Yoshida
2002-07-18
![]() , is a representative radiation in many astronomical
environments that produces high energy X-ray/
, is a representative radiation in many astronomical
environments that produces high energy X-ray/![]() -ray.
-ray.
![]() as defined by
as defined by
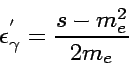
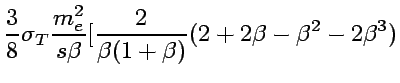
![$\displaystyle -{1\over \beta^2}(2-3\beta^2-\beta^3)\ln{1+\beta\over 1-\beta}],$](img121.png)