High energy radiation from various classes of galactic and extragalactic objects has been observed for nearly 30 years. A large fraction of galactic sources is associated with neutron-stars: rotation powered pulsars, accretion powered pulsars and so on. Neutron stars are very small by astronomical standards. Our own Sun's radius is 100 times bigger than the radius of the Earth. However, the typical radius of a neutron star is thought to be only about 10 kilometers (6.25 miles). At the same time, a neutron star contains up to 1.5 times as much matter as the Sun, making the density of these objects tremendous. A teaspoon of neutron star material weighs about a billion (1,000,000,000) tons. This much matter in such a small space creates an enormous gravitational field, so powerful, in fact, that it can bend light!
Pulsars are highly magnetized rapidly spinning stars schematically
shown in FIG. 8.
The strength of magnetic field is estimated
by the assumption that the rotation energy of the neutron star
powers the radiation originally via the magnetic dipole radiation.
The rotation energy ![]() of a neutron star
of inertia moment
of a neutron star
of inertia moment ![]() rotating with angular velocity
rotating with angular velocity
![]() and its time derivative read
and its time derivative read
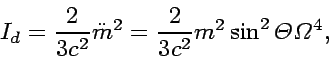 |
(50) |
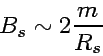 |
(51) |
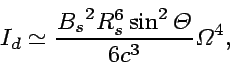 |
(52) |
![\begin{figure}\centering\includegraphics[width=.8\textwidth]{p_diagram.eps}
\par\end{figure}](Timg212.png) |
Detection of radio, X-ray, and ![]() -rays from pulsars has indicated
that high energy radiation takes places in pulsar magnetosphere.
Process relevant for production and transfer of high energy radiation
in a pulsar are:
-rays from pulsars has indicated
that high energy radiation takes places in pulsar magnetosphere.
Process relevant for production and transfer of high energy radiation
in a pulsar are:
Electrons are thought to be accelerated to relativistic energies
and very high energy (VHE) ![]() -rays are produced via curvature
radiation. Generated photons pair-produce
-rays are produced via curvature
radiation. Generated photons pair-produce ![]() pairs
by either magnetic pair creation (such as Crab Pulsar)
or photon-photon pair creation (like Vela pulsar).
These secondary electrons are subject to the synchrotron radiation.
pairs
by either magnetic pair creation (such as Crab Pulsar)
or photon-photon pair creation (like Vela pulsar).
These secondary electrons are subject to the synchrotron radiation.
Now we can estimate the energy of ![]() -rays radiated by
the accelerated electrons in the magnetosphere.
Equation 47
gives the typical photon energy of synchrotron photons
in the magnetosphere of
-rays radiated by
the accelerated electrons in the magnetosphere.
Equation 47
gives the typical photon energy of synchrotron photons
in the magnetosphere of ![]() Gauss.
Using
Gauss.
Using
![]() rad/sec/Gauss,
rad/sec/Gauss,
![]() MeV s and that
MeV s and that ![]() keV,
we obtain
keV,
we obtain