The electromagnetic (EM) process are always related to
photons because they are the particles to carry energy and
momentum in electromagnetic interactions. Therefore, some
of the EM reactions would GENERATE photons, such as
pair annihilation
![]() , the inverse
process of the pair creation. Electrons are also
producing photons by interacting with magnetic field,
which is called synchrotron radiation, the representative
radiation process that can be described in the standard context
of the classical electromagnetic theory.
, the inverse
process of the pair creation. Electrons are also
producing photons by interacting with magnetic field,
which is called synchrotron radiation, the representative
radiation process that can be described in the standard context
of the classical electromagnetic theory.
Now let us derive the radiation intensity, i.e.
the radiated energy per unit time
![]() .
First we expand the treatment of the dipole radiation
given by Eq. 8
to the super-relativistic condition that particles are moving
almost at speed of light.
The dipole
.
First we expand the treatment of the dipole radiation
given by Eq. 8
to the super-relativistic condition that particles are moving
almost at speed of light.
The dipole ![]() is related to acceleration
is related to acceleration ![]() by
by
![]() and Eq. 8
gives the total radiation intensity as
and Eq. 8
gives the total radiation intensity as
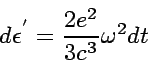 |
(37) |
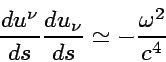 |
(39) |
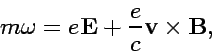 |
(41) |
In the uniform ![]() field, an electron's movement
is characterized by the synchrotron frequency
field, an electron's movement
is characterized by the synchrotron frequency
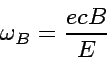 |
(43) |
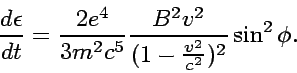 |
(44) |
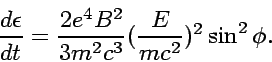 |
(45) |
Energies of the radiated photons are narrowly distributed
around