Transportation of the VHE $\gamma$-ray in the Universe

The Universe is not empty but filled with Cosmic Microwave Background (CMBs). For very high energy (VHE) $\gamma$-rays and electrons, our Universe is not transparent any more but rather opaque because they yield electromagnetic (EM) cascades in extragalactic space as the electrons and photons collide further with the CMB photons. A high energy photon pair-produces electrons in the CMB photon field. An electron kicks out a CMB photon to high energy range via the inverse Compton scattering. These two channels mainly drive the EM (electro-magnetic) cascade recycling energies to much lower energies with growing number of photons and electrons. Schematically,

$$\gamma_{VHE}\gamma_{CMB} \to e^+ e^-$$

$$e^{\pm}\gamma_{CMB} \to e^{\pm}\gamma_{VHE}$$

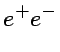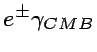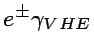The CMB is not only the universal diffuse radiation backgrounds which are involved in the EM cascades but the radio and infrared-optical (IR-O) backgrounds also play an important role in the cascade depending on energies of high energy particles in the cascade. The threshold energy of pair production is given by

$$\epsilon_{th}^{\gamma\gamma}= {(m_ec)^2\over \epsilon_{rad}}... ...t({\epsilon_{rad}\over 10^{-3}\mbox{eV}}\right)\quad \mbox{eV}$$ (33)

where $\epsilon_{rad}$ is energy of a photon in the background radiation field. Therefore the reaction with the CMB opens when $E\geq 3\times 10^{14}$ eV, wheres a typical radio photon ( $\epsilon_{rad}\sim 10^{-8}$ eV or less) can pair-produce electrons if $E\geq 3\times 10^{19}$ eV and a IR-O photon reacts effectively in lower energy regime of $E\leq 10^{13}$ eV. Since we do not accurately know intensities of the radio and IR-O background, the estimation of the EM flux always has some uncertainties. In other words the precise measurement of the flux would provide some insights into the intensity of these background radiations. Thus exploring VHE $\gamma$-ray propagation is also important to infer the parameters of the universal radiation fields.

In case of the collisions between VHE $\gamma$-rays and CMB photons, the differential cross section of pair creation can be rather easily obtained. Not let us calculate the cross sections to see the general characteristics of the EM cascades driven in the Universe. The energy of pair-produced electron in CMS, $\ast{E_{-}}$, is equivalent to $\sqrt{s}/2$. Using Eq. 27 and the fact that energy of $\epsilon_{\gamma}$ is orders of magnitude higher than that of CMB $\epsilon_{CMB}$, we find

$$\gamma_c = {\epsilon_{\gamma}\over \sqrt{s}}.$$ (34)

Then we obtain

$$\eta_{-}\equiv {E_{-}\over \epsilon_{\gamma}} = {1\over 2} \left( 1+\sqrt{{s-4m_e^2\over s}}\cos\Theta \right).$$ (35)

Here $\eta_{-}$ is the dimensionless energy of the electron normalized by primary energy of VHE $\gamma$-ray $\epsilon_{\gamma}$. Then Eq. 32 reads

$${d\sigma\over d\eta_{-}}\simeq {2\pi m_e^2 r_e^2\over s}\lef... ...-\eta_{-}\over \eta_{-}} + {\eta_{-}\over 1-\eta_{-}} \right].$$ (36)

Pair-produced electrons are subject to the inverse Compton scattering with the background photons. The differential cross section is given by Eq. 30.

Figure 7: The energy attenuation length for cascade photons as a function of energy. The length for protons is also shown by the dotted curve for comparison.

FIG. 7 shows the attenuation length calculated by the cross sections of the relevant reactions, indicating how long VHE $\gamma$-rays can travel in the extragalactic space. One can see that VHE $\gamma$-rays with energies of $10^{15}$ eV can only run over $\sim 10$ kpc that is equivalent to the dimension of out Galaxy. It implies that we are not able to see an extragalactic part of the Universe in the VHE energy range by photons. The structures seen in the figure at $10^{13}$ and $10^{20}$ eV are formed by interactions with IR-O and radio photons, respectively, as described above. It should be remarked, however, that, energies of ultra-high energy (UHE) photons above $10^{19}$ eV would not be degraded rapidly in the EM cascade. As the pair production cross section has local maximal at $\eta\sim 0$ and $\eta\sim 1$, either of pair-produced electrons carries most fraction of energy of primary UHE $\gamma$-ray. The leading electron transfer most of its energy again to the photon via the inverse Compton scattering as you see the cross section becomes larger in $\chi\ll 1$ regime in Eq.30. Thus leading photons and electrons would maintain their energies longer than nucleons do.